为什么长方体上的三个点不能唯一确定一个长方体?

本文是随手写的证明，仅抛砖引玉。在下虽已简单审阅思考了几遍觉得大致无误，但仍然不敢保证不存在证明或者说理上的失误，请阁下带着审慎的目光阅读。如有疑问请留言。

确定一个三维空间中的任意长方体至少需要多少参数？

一个三维空间中的任意长方体有9个自由度

• 3个用于平移
• 3个用于旋转
• 3个用于长宽高(缩放)

所以表示这样一个长方体至少需要9个数值

如何用9个参数唯一确定一个长方体

通俗法

先使用6个数值，表示长方体的两个顶点，定义这两个顶点的连线构成长方体的高。

则长方体的物理约束让我们知道”长方体顶面和底面所在的平面”

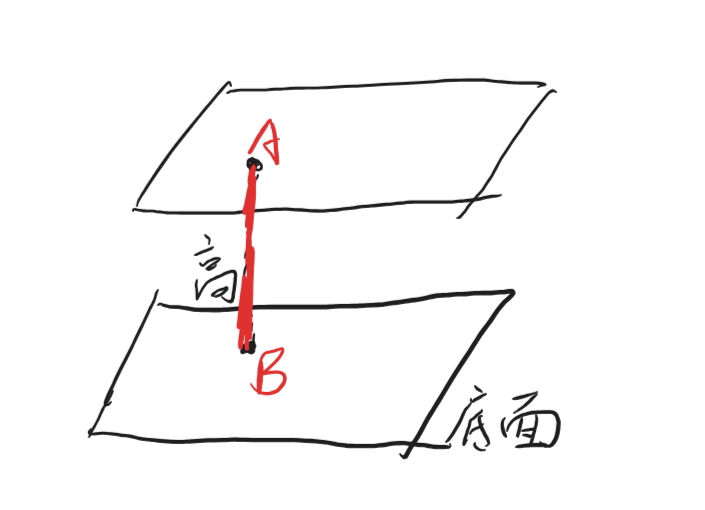
以关注底面为例，我们只需要在底面定义一个全新的基(这个基可以来自于原来三维空间基的一种人为定义的映射，所以唯一确定)，然后使用一个二维向量表示出其中一条边的方向和长度，最后补上一个参数表示与它垂直的另一条边的长度。

分别需要使用2个参数和1个参数。

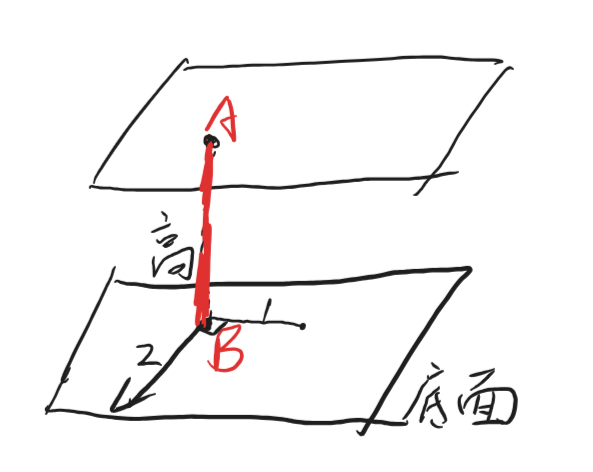
于是我们使用9个数值就得到了如图所示的长方体的4个顶点，而后使用常规方法即可得到长方体。

如果您觉得这种方法看着不严谨，可以看看下面的数学法。

数学法

设

• 表示长方体几何中心的位置

• 表示其沿自身三个主轴的长度，即长宽高

• 表示这个长方体的欧拉角，即朝向。在这里使用Z-Y-X顺序，表示长方体从一个自身主轴与坐标轴对齐的状态，先绕自身Z轴旋转，再绕自身Y轴旋转，最后绕自身X轴旋转

充分性(重建过程):

先在原点处创建标准长方体，尺寸为，并且长宽高分别与X、Y、Z轴平行。

即, 其八个顶点坐标为：

则我们有了一个几何中心位于原点的长方体，这长方体的形状和目标长方体完全一致。

然后根据​对长方体进行旋转即可(左乘旋转矩阵)

• 绕Z轴旋转 ​ (只需要计算坐标基旋转后的状态):

• 绕Y轴旋转:

• 绕X轴旋转:

对于之前得到的分别依次左乘上述旋转矩阵，就能得到几何中心在原点，但朝向完全正确的长方体。之后只需要对每个顶点坐标加上几何中心的坐标完成平移，即可重建长方体。

为什么不能用三个在长方体上的点来重建一个长方体

ps: 如果三个点不是在长方体上的点，与长方体无直接的几何关系，那和直接存储数值又有何异？私以为没有讨论价值，这里只讨论三个点在长方体上的情况。

核心原因：三个在长方体上的点存在内生约束，它虽然有9个数值，但自由度并非9，有损失，无法表示需要9个自由量表示的长方体。

只需要证明三个点的坐标数值至少存在一个自由度损失：

若三个点均为长方体顶点

首先我们可以在长方体上建立它自己的内生坐标系，方便讨论。

情况1：存在两个顶点的连线构成了长方体的一条边AB

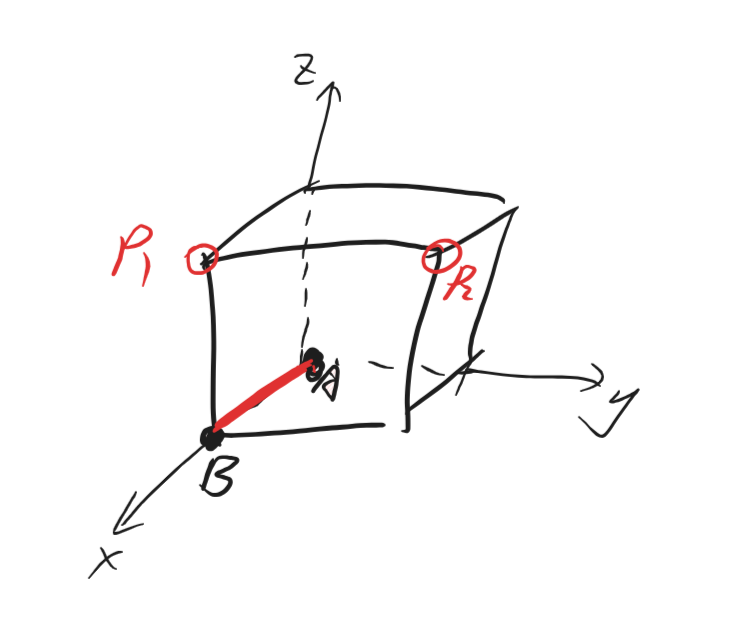
根据对称性可知，第三个点实际上只有P1和P2两种情况。

因为AB垂直于P1P2B平面，所以当AB已经确定的时候，P1与P2的x坐标是冗余的！这意味着至少存在一个自由度损失，相当于至多也就只有8个有用的数值，所以无法表示有9个自由度的长方体。

情况2：存在两个顶点的连线构成了长方体的一条面对角线AB

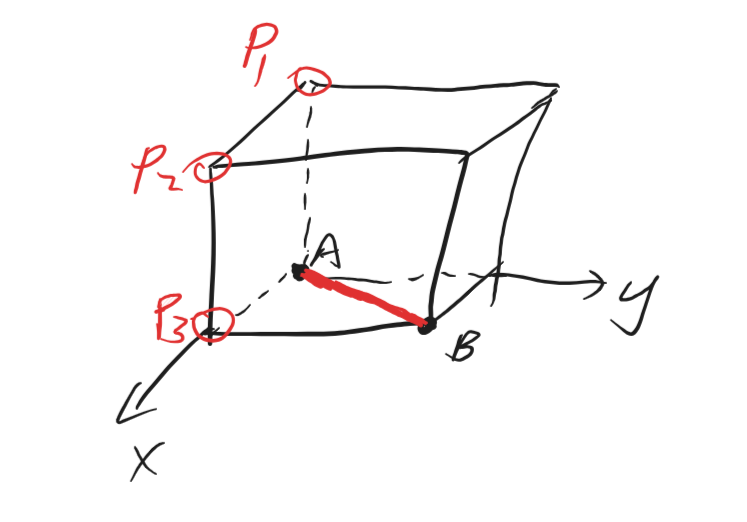
由对称性可知，第三个点实际上只有P1P2P3三种情况，并且P1和P3的情况直接退化到了前面讨论过的情况1：存在两个顶点的连线构成了长方体的一条边AB， 所以实际上只需要考虑P2。

如果第三个顶点取P2的话，则ABP2包夹的顶点(对应图中P3位置)可能出现在平面ABP2的两侧，无法唯一确定。

• 但是抛砖引玉：分别以AB，AP2，BP2为直径做球，交点即为解，但根据对称点，有两个交点
  • 然而即便如此，在工程上只需要人为定义稳定地取其中某一侧的解，则仍然可以构成一一映射关系——每个三点组可以映射到一个长方体，而每个长方体也唯一映射到一个三点组(一个长方体可以切出两个如图所示的面，但是在规定“只有位于平面的才算解”时，只有一个面是有效的)。但是那是另话了(实现起来可能会很麻烦)。不过，在数学上不能唯一确定但在工程上能够形成一一对应关系，确实会令人觉得很神奇。或许也有一些取巧的成分在里面吧

情况3：存在两个顶点的连线构成了长方体的一条体对角线AB

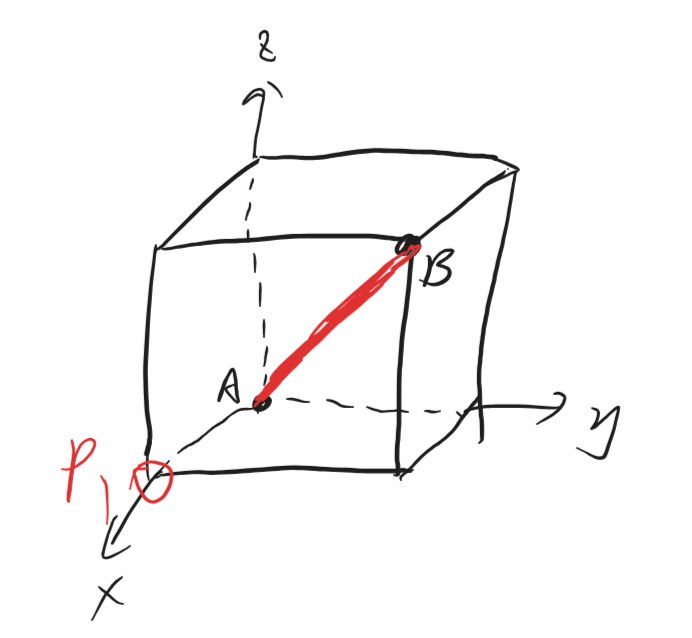
由对称性可知，实际上第三个点只有P1一种情况，而这种情况AP1构成了边，又退化到了情况1：存在两个顶点的连线构成了长方体的一条边AB，故而无法重建。

若三个点中至少有一个点不是长方体的顶点

核心思想：若点不是顶点，反而携带的信息量更少了，故而更不能重建了。

ps: 该部分或有不严谨的地方，请理性审阅

情况1：有一个点在边上(不含顶点)

重建长方体的目标可以建模成求解图中P, L1, L2, L3， 这都是最后重建长方体需要且必须能够解得的变量。

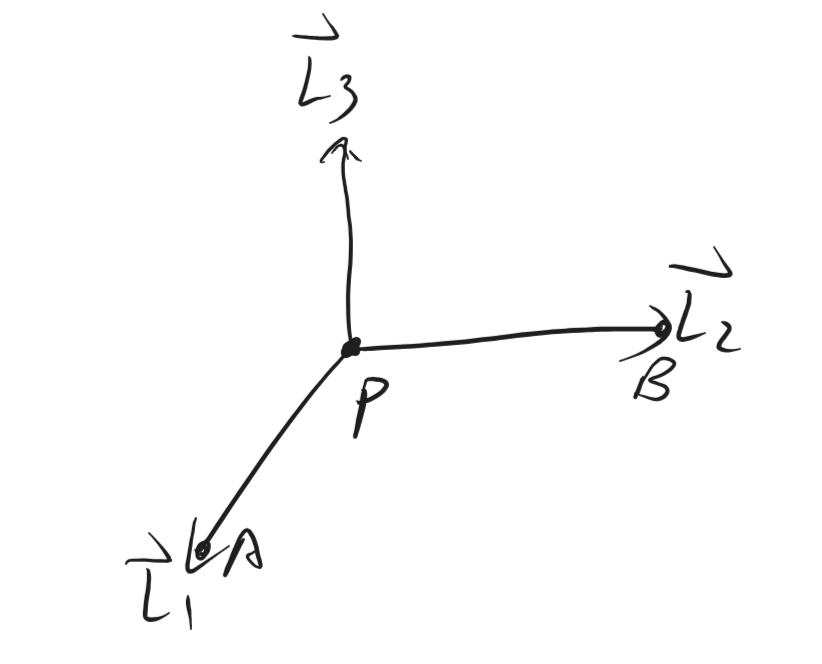
所以我们用这几个基础性的变量来表征每个点为我们带来的信息。

若得到的点是顶点，例如A，得到的方程实际上为:

• A = P + L1

但若得到的点是边上的点，例如PA上的点T，则得到的方程实际上为：

• T = P + t L1

其中t是全新的未知的变量，实际上并不会增加整个方程组的确定性，反而会引来更多的未知数。

情况2: 有一个点在面上(不含顶点)

延续情况1的逻辑，若得到的点是面上的点，例如PAB上的点T，则得到的方程实际上为：

• T = P + u L1 + v L2

其中u, v都是全新的未知的变量，实际上也并不会为整个方程组带来更多的信息。

综上所述，仅仅使用长方体上的三个点重建(唯一确定)长方体是在数学上不可行的。工程上引入新的规则那咱不管